Systematics

an introduction by Anthony Blake

Systematics was developed by John Bennett in the 60’s working with a variety of people over many years, including Anthony Blake. Through the help of managers such as Saul Kuchinsky, he introduced systematics to the business world, but only on a very small scale. Given the present turmoil of new thinking systematics assumes a new significance as a way of understanding complexity in flux and uncertainty. This introduction is to give an overview, not going into any details. But even from this brief statement, it should be possible to make a start. Practitioners of systematics are formed into a loose association called ‘UNIS’ that may grow into The Guild of Workers with Systems – a ‘guild’ because it is more a craft than a science. We welcome connection with other workers in systems, no matter how divergent they may be from the principles of systematics.

Systematics links with structural communications.

“A system is a set of independent but mutually relevant terms.”
J. G. Bennett

Number Systems

Systematics was the name given by John Bennett to the study and application of systems based on the integral numbers 1, 2, 3, etc. Such systems are basic ways of seeing that have universal meaning and can be found in every culture from ancient times right up into our own. Perhaps because such systems are to be found in very many places — and often accepted unconsciously as part of cultural traditions — their importance and usefulness has not been appreciated before. In recent times, the pressures of handling complexity have grown so much that these systems need to be made more conscious, and studied in their own right, as an aid to understanding and achieving the organisation of complexity.

In the twentieth century, systems thinking of many kinds has come to the fore. Some of this is very technical and there is no generally agreed method amongst the variety of theories and applications. In contrast, systematics draw on the wealth of accumulated wisdom of the ages and offers a fairly simple line of approach. This is not to put aside the efforts of such people as Bertalanffy, for example, or to ignore the important steps taken in understanding complex, emergent, self-organising systems by people such as Kauffman. It is only to urge that we take advantage of what is available to us if we just look around with a ‘systematic eye’.

Systematics is essentially holistic. The term is associated with the pioneering work of Jan Smuts, whose Holism and Evolution remains seminal. In this theory, Smuts argues that we can discern in evolution a progression of organisation, from simple to ever more complex and all-inclusive, from matter through life to mind and society. Bennett took on this theme of a progression but expressed it in more general and abstract terms as a progression of systems from simple wholeness to ever more highly structured kinds of organisation. He even suggested that we could regard God as the ‘infinite system’. The steps along the way were marked by the number systems as a series: 1-fold, 2-fold, 3-fold, etc. So wholeness was not single valued. What it meant depended on what system we were in.

The idea that wholeness is relative is simple but profound. A way of thinking about this is by taking the systems as referring to a progression of being. As the order of the system increased, so would then the degree of being. Being, in Bennett’s view, was a matter of ‘degree of inner togetherness’. So, we can visualise a progression from a loose association of content to a deeper and deeper intensity of inner togetherness.

We use Bennett’s concept of being as a guide because it does turn out to be very important that we do not look on systems as if they were describing things from the outside. Systems are not scientific models but insights into degrees of organisation. In his first major essay in this field, The Dramatic Universe (Vol. I) he deals with the universe as a totality of twelve levels of existence, each more ‘potent’ than the level that precedes it. Later, he saw that the same principles applied to any living situation, big or small. We could look, for example, at a human enterprise in such terms. Everything ‘begins’ from simple wholeness and has the promise of progressing in depth to something significant for the greater whole.

The starting point of the series of systems, called the monad, is not a metaphysical absolute but simply ‘where one starts’. It is any simple, immediate sense of wholeness that is relatively undifferentiated and is rather like a ‘field’ of meaning. Usually, it is reached by a process of ‘dissolving’ our usual distinctions. It is not an object but unity in diversity and diversity in unity.

When Bennett came to think about the number systems, he tried to put aside traditional forms of them, as far as he could. This was to make as fresh a start as possible — and also to see whether we had some basis in the very nature of our experience for realising what the systems were like. Since that time, we have found it possible to return to traditional understanding and gain insight from them. The exercise of trying to think — or intuit — the systems for oneself, without recourse to extant forms, is always to be recommended. But there has to be dialogue with others, too, because systematics proves of greatest value in bringing people together in common purpose and vision.

Once one has thought for oneself and then with others, it is possible to recognise insight everywhere, in ancient cultures and in modern ones also. It is quite possible that no one has exactly the same way of seeing a system as anyone else. Nevertheless, the more one works at it, the more one is able to appreciate the diverse points of view and make use of them. Because the systems are based on the integers, they are easily recognisable, even when appearing under different guises. We can, for example, find our way between the Christian Trinity, the guna theory of the Indian Samkhya and the Hegelian dialectic, simply because they are all ‘threefold’. They are not identical — but they illuminate each other.

Working with the systems, one tends to acquire favourite modalities of them; but it is always important to seek out challenges to one’s understanding. There is no authority that dictates what the systems should be like. They are useful if they ‘make sense’ for you and those you work with.

History

The history of systems is as extensive as the history of human thought. It would take volumes to summarise it. Suffice it to say that, from the very beginning, humans have sought out patterns of meaning of universal import. One of the very first such attempts was in finding heavenly patterns for which there were ‘echoes’ on the earth. The movements of the stars and planets were of crucial importance in deriving a structural language for describing significant events on earth. One of the most basic such forms concerned the cycle of the seasons, that divided the zodiac — the circle of the ‘animals’ — into four parts. This became elaborated into the twelve houses of the zodiac. Set against these were the movement of the planets, a sevenfold system. By the combination of the two, the most elaborate structures could be coded. Incidentally, it is most striking that ascribing the stars to animals and the planets to gods was universal throughout the earth even as far back as 10,000 years ago at the beginning of agriculture.

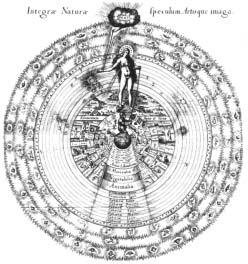
The coding of information was a great art. It came down to us through stories and hence ‘texts’ that only now we are beginning to see again as highly refined structures of meaning. Even before writing, poems and stories were constructed to facilitate memory and accuracy and enhancement of meaning. Briefly, the method was to conceive the sequence of a story, hymn or poem as if arranged in a circle. The two halves of the circle – ‘left’ and ‘right’ – signified two different levels or kinds of meaning of the same elements, repeated again.

Parts of the story on the right were correlated with parts on the left. Some of these correlations were complex, yet based on repeating patterns, and therefore capable of being understood.

The circular arrangement was visualised and not given in the text. One had to be able to discern it. As one had to be able to discern the inner connections. This was probably the origin of what we now talk about as the ‘exoteric’ and the ‘esoteric’. The exoteric could only follow the story in a linear sequence and the inner connections were only felt or registered unconsciously. The esoteric could ‘see’ the inner connections and appreciate more consciously the depth of meaning. One widely known example of this has only just been understood once more: the sequence of the days of the week — associated with the seven ancient planets — appears arbitrary unless one sees that it is based on reading a sequence through inner connections. The actual order — arranged in the circle – is that of observed angular velocity.

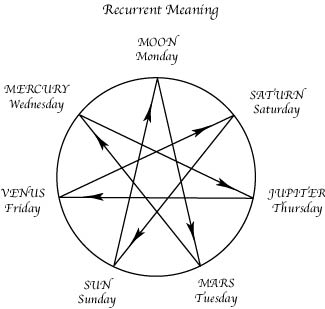
The forms of inner connection, like the sense of the ‘heavenly pattern reflected on the earth’, have come down to us in astrology in one form and in the remnants of the ‘art of memory’ in another.

Philosophy has its roots in concern with intelligibility. It was led to consider the ‘least intelligible’ as inchoate material from which the cosmos was fashioned or emerged, drawn into being by the ‘supreme intelligible’. There has always been some sense of a scale from least to greatest, from matter to spirit. The nodes on these scales, represented in a variety of ways according to time, place and culture, can be marked out as the series of systems. Both in east and west we find the sentiment: ‘from the one comes forth the two, from the two comes forth the three, and . . .’. The ‘and’ has different versions. In one it is the ‘ten thousand’, in another it is ‘the one again’. Naturalistic views of evolution and spiritual views of perfecting are in close accord, once we see the universality of the scale or progression.

Matter first appears as chaos because there are no distinctions in it. This is how it is depicted in Genesis, before God says ‘Let there be light!’ and divides the light from the darkness. Matter, from ancient times, has been a name for the first system. The ‘light’ is also consciousness. Light and dark, conscious and unconscious, are undivided but distinct. Everyone knows of yin and yang but the same system — the second or dyad – is to be found in the complementarity interpretation of quantum mechanics.

The third is equally ubiquitous, dealing with how dynamism, or change is possible. The greater the number of systems we entertain, the more difficult it is to remember; so they are often combined into structures of meaning, as in the sacred texts we mentioned above. They are also contained in pictorial sequences, such as the famous Ox-herding series. Or mathematically integrated in such forms as the Enneagram spoken of by Gurdjieff (the enneagram is a form of what we call N-gram, briefly described later on).

Raymond Lull was concerned with what we now call ‘knowledge organisation’. His approach is systemic, based on number, but also appears in terms of circles, triangles and squares (monad, triad and tetrad). He even comments that these have different champions and compete! An interesting notion, since it appears that different people favour different systems, just as different cultures do. Concerning the last, we can recall that the Muslims hated the Christians because they said God was 3 and not 1, the Buddhists pegged God as zero and the Christians themselves persecuted the Cathars because they were dualists!

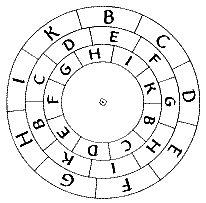
Raymond Lull’s experiments with mutually rotating disks representing systems came down through the Middle Ages to appear in a different guise in Liebniz’s ‘universal calculus’ — an effort to calculate philosophical questions instead of just arguing about them. His genius was to look into how we generate ideas by combinations of other ideas — basically triadic.

Throughout the traditional cultures of the world, systems abound. A great favourite is the tetrad, the 4-fold system. Hence, the four rivers of Paradise in the Bible, the four winds or directions of the Amerindians, the four elements of the Greeks and so on and so on. We can also find pictorial sequences in tens (incidentally also the number of the Kabbalistic Tree of Life) and the 8-fold path of enlightenment, use of the body as a metaphor with its different organs as in the 7-fold chakra system of Indian psychology.

With the rise of analytical science from Newton, Descartes and Galileo much of this was pushed into the background. The great twentieth physicist Wolfgang Pauli regarded this move as a disaster. Since he was working with Carl Jung at the time, he expressed this as physics adopting the triad instead of the tetrad — Jung himself being deeply concerned with the transition in Christian culture from the 3 of the Trinity to the 4 that included the Virgin Mother. According to Pauli, the triad encouraged mathematical abstraction, at the expense of the tetrad or quaternary that looked into the transformation of matter and was foremost in alchemy. The loss of ancient intuitive patterns was recompensed by extraordinary advances in knowledge. It was if the patterns went back into the unconscious. They still had an influence but from behind the scenes (thus, for example, Newton’s Laws of Motion form a triad and his work on colour was dominated by a sense of 7-foldness). Part of Jung’s work was to bring them back from the unconscious and acknowledge them again.

Philosophers such as Descartes, Kant and Hegel sought after basic underlying ‘categories’ of thought that seemed to be inherent in anything meaningful. In retrospect, they can be seen to be carrying on the tradition of Raymond Lull. While any fixed expression of these is suspect — just because it is fixed — the quest is not useless. Bennett himself took up the challenge of one of his teachers P. D. Ouspensky — to ‘think in new categories’. This means to bring out what is underlying our world views, just in order to see beyond our present frame of reference, the patterns of thought which regulate our thinking (and experience) usually in an conscious way. Number systems have the advantage of mapping a great deal of our modes of understanding and also the merit of being evidently distinct from each other. Their versatility — both separately and in combination — is such that a very great deal of our thinking can be made transparent and accessible through them.

The mechanistic universe world view reached its apogee in the nineteenth century when physics and biology were forced to restore something of the abandoned wholeness and structure. Relativity, evolution, thermodynamics, quantum theory were the start of a new wave of science. With it came a resurgence of ‘organic thinking’ as represented in the philosophies of Peirce and Whitehead. Peirce himself was aware of systems and spoke of how different people prefer one, two, three, four or five as their mode of explanation — he himself favoured the three-fold system. Whitehead moved from the foundations of mathematics to a philosophy of organism based on a new category of creativity. This set the scene for the later arising of interest in complex, emergent, self-organising systems. Whitehead also outlined the basic principles of progression by which higher term systems evolve out of smaller term ones. Such a view was echoed by Jan Smuts.

The present scene is complex and even chaotic, since there exist a variety of approaches to systems. Some involve cybernetics, others complexity theory, yet others knowledge organisation, etc. Psychological theory abounds with triads and tetrads. Engineers such as Bucky Fuller and Arthur Young espouse deep theories based around number systems. There is new interest in the ancient cosmologies of Pythagoras and Plato. The ‘esoteric’ knowledge of systems that was marginalised in the seventeenth century has re-appeared, but still in a very fragmented way. Thus we may come across extraordinary yet very much isolated geniuses such as Charlotte Bach and William Pensinger even more marginalised than Fuller or Young.

Egyptian Quaternary from Charlotte Bach’s ‘Concerning the Invention and Evolution of Writing’

Studies of the brain suggest that it is capable of a synthetic balance between processes concerned with parts and processes concerned with wholes — what William Blake called ‘Two-fold vision’. The kind of balance we have seems to be affected by historical, cultural forces. We appear to be undergoing a new synthesis.

Number Systems

An assumption made in systematics is that the systems are relevant to any whole. This does not mean that they are thought to contain everything of meaning. It is their simplicity and abstractness that renders them so versatile.

Though we have spoken of a progressive series of systems — 1, 2, 3, 4, 5, etc. — it is by way of an hypothesis. As the number of the system increases, so does its possibility of decomposition into simpler systems also increase. However, the hypothesis is a valuable heuristic. One way of thinking about it is in terms of an increasing number of ‘dimensions’ of thought. Here, it is striking that twentieth century has seen many attempts to broaden the scope of dimensionality in physics.

Reverting to the analogue with degrees of being, we can think of a progression in the ‘degrees of freedom’ that a whole exhibits. This fits with the idea of life arising in an increasingly autonomous form, reaching a (perhaps temporary) summit in intelligence. Speaking of living forms, it is good to remember that the systems are not isolated quasi-entities, but are open systems, coupled with their environment and not separate from it. Perception and intelligence must emerge as properties of systems themselves.

In a system of order N, represented simply as [N], there are N distinct elements, or N dimensions of discrimination, or N degrees of freedom. Each of these ways can reflect into the others and, as a consequence, sometimes a system is thought of as [N] and sometimes as [N-1] or [N + 1]. For example if we have N parts then there are N-1 degrees of freedom. The N elements are not ‘parts’ in the usual sense of that word, though they may be thought of as ‘fractions of the whole’. The number and characters of the elements are proper to the system in which they appear. Thus, it is not correct to add on another element to make a higher term system. The system has to be ‘resolved’ into a higher order by a higher order act of discrimination.

The idea of ‘fractions of the whole’ distinguishes number systems from assemblages of parts working together. Each number division N of the whole creates a definitive characteristic and, because there are N terms, each of them assumes a different mode of that characteristic. Thus, the triad resolves the whole into three impulses, distinguished as: affirmative, receptive and reconciling.

In the 1-fold system, the Monad, there is only one element — of wholeness – with the character of diversity.

In the 2-fold system, the Dyad, there are two natures, sometimes called the ‘infinite’ and the ‘finite’ poles.

In the 3-fold system, there are three impulses, sometimes called affirmative, receptive and reconciling.

In the 4-fold system there are four sources, sometimes called ideal, actual, masculine and feminine.

In the 5-fold system there are five foci, sometimes called ‘limits’ representing the outer and inner, higher and lower, and the centre.

And so on. These various descriptive words draw on particular paradigms of the systems (as in the above example) and are not exhaustive. What matters is to be able to translate between different versions corresponding to the same system.

Representation of Pentad from Bennett’s ‘The Dramatic Universe’

Thus, the elements of a system are not just objects. They are qualitatively different from system to system. This is because what they are depends on each other. Bennett spoke of the elements as ‘mutually relevant’ to each other. They can be said to be of the same genus but of different species within that genus. Following this taxonomic analogy, we can speak of the system as a whole as an ‘order’. It is only the number N of the system that determines all this.

The basic idea is that if, for example, we have only two ‘fractions of the whole’ then this is a different kind of reality or view from when we have three. Each system, then, constitutes a way of seeing reality in its own right. When people converse or exchange views, it is usually not clear from which system they are speaking. Thus, confusion often ensues.

The coding of information according to number systems is a powerful way of gathering together insights of the same kind. Each system allows for variations, but they can all be contained in the same form. The systems are not formulas but guides. Bennett used the term ‘sets’ in defining number systems because he was following on the tradition of the mathematician Cantor: Cantor defined number by means of equivalent sets without regard to content. Sets said to be of equal number have members that can be mapped one-to-one with members of other sets. Their only similarity is in number. Bennett went further in stating that the meaning of every member of a number system [N] was the same for any such number system [N].

Number systems differ from the systems of General Systems Theory because they are not hierarchical. However, we can decompose a high order system such as the 12-fold one into three tetrads or four triads, exchanging depth for convenience. The first twelve systems can also be arranged into a circle, such that the 12-fold system appears at the top, and we find correlations between [5] and [7], [4] and [8], [3] and [9], [2] and [10] and [1] and [11].

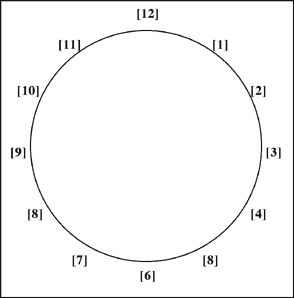
We might take the number systems to be analogous with the different kinds of ‘force’ studied in physics, or with the fundamental particles also studied. The possible forms that can arise by means of combinations of systems is immense. In real life situations, as Bennett insisted, we are unlikely to come across ‘pure’ systems but only systems together with other ones. It takes a special effort to deal with only one system at a time.

There is also the internal structure of systems. Mechanistic systems thinking derived from engineering tends to think of systems as consisting of various parts connected together. The internal ‘togetherness’ of systems is more subtle than that. There are not connections separate from things connected. David Bohm, the physicist, suggested that instead of the metric kind of space we are used to, we might consider a more topological kind of space, in which different regions are ‘present’ to each other; in which case we would not need to think of connections at all but only kinds of ‘mutual presence’. Such concepts are a reflection of being rather than of function.

The ‘connectivities’ present in systems may be considered as sub-systems in their own right — that is, as modes of togetherness. Thus systems have ‘smaller systems’ within them and can be thought of as nested totalities of systems. In the triad, for example, which is 3-fold, there are three ‘monads’ (A, B and C) and three ‘dyads’ (AB, BC, CA) as well as one triad (ABC).

What a ‘monad’ or ‘dyad’ means depends on its systemic context. A ‘dyad’ in a triad is not the same as one in a tetrad, and differs from a ‘dyad’ taken in its own right. In other words, as we come more these days to accept, the meaning of any feature depends on context.

Thinking in this way, we can see that there is a totality of nested systems representing the ‘greater whole’. This gives a valuable starting point for investigating organised complexity. Though it is possible to treat the systems as ‘atomic’ they have their greatest meaning in a more organic understanding.

Studies of the internal structure of systems can be made in a mathematical way — for example, by looking at ‘partitions’. ‘Partitions’ are the many ways in which a given number be decomposed into an addition of smaller numbers. Thus, for example,

6 = 5 + 1 = 4 + 2 = 3 + 3 = 4 + 1 + 1 = 3 + 2 + 1 = 2 + 2 + 2 = 1 + 2 + 3 = 1 + 1 + 4 = etc.

Partitions have been studied in a formal sense but little use has been made of them in practical applications.

Systematics has come into play in more pragmatic realms simply as an embodiment of accumulated wisdom. For example, time and again we can come across ‘complete structures’ in 7-fold schemes. These have arisen out of practical experience, but no one knows ‘why’ these turn out 7-fold. Similarly, there is pragmatic evidence that the maintenance of any operating system requires four roles. Again, no one knows ‘why’. It seems that systems embody an understanding that at present escapes our powers of analysis. In all such cases, we find that the given system is normative, in that all the terms must be actively present for the task to be fulfilled well.

We emphasise the pragmatic also because systematics concerns what we can ‘do together’. People coming together for a task inevitably articulate themselves into distinct roles — to provide an adequate number of independent degrees of freedom and sources of information. Systematics does not conform to hierarchical modes of organisation but supports a multi-faceted kind of action. It is therefore highly relevant to our modern concerns over learning how to co-operate in the management of complex tasks. In a ‘completely realised’ group of N people, there will be N distinct roles, without duplication, within any given present moment totality. This has been taken up as a method in N-logue (see below).

Method

The progression of systems gives an heuristic method that is both analytical and intuitive.

The first step — pertaining to the monad – is to gather information as diverse as possible and as far ranging as possible, from a variety of sources, all clustering around the theme of interest, or expressing the world under review. The discipline here is to gather without any gradations of importance or any kind of valuation or judgement. If we are already fixated on a ‘problem’ or line of approach, this serves as a corrective. It is tantamount to deconditioning. It requires an almost aesthetic sense of relevance rather than a conceptual one. Whitehead was a great proponent of this approach. It is to regain a sense of ‘raw experience’. Charles Sanders Peirce refers to ‘the consciousness of a moment as it is in its singleness, without regard to its relations — whether to its own elements or to anything else’.

The monadic stage requires discipline. It is similar to but different from ‘brainstorming’ -requiring a greater sense or ‘feeling’ of wholeness. If worked at it can of itself provide important insight. All the time our minds are tending towards making distinctions, choices, judgements, etc. and these need to be suspended. This kind of suspension has been recognised in a variety of ways, though not considered together as they can be in systematics. For example, it corresponds to the ‘relaxed but alert’ state of the mind that is open but not passive. It is the ‘putting into brackets’ of the phenomenological method of Husserl. It is similar to the ‘naturalist’s trance’ practised for example by E. O Wilson. In anthropological terms, it is the participation mystique. It is the underlying condition for true dialogue. And so on. It is sometimes very hard to restrain oneself from falling back into problem-solving attitudes, or jumping to conclusions. This has been studied by as diverse people as the mystic Krishnamurti — who was a great influence on Bohm — and Ansthuller, the originator of the method of innovation known as TRIZ, who states categorically that innovation cannot begin from a defined problem.

The dyadic stage of investigation requires a jump into a totally different mode from the monadic stage. It is to seek out the core contradiction, paradox or dilemma. This is detected by working through differences of point of view to find the pair that are always together but contradict each other. In other words, in spite of contradicting each other, we cannot have one without the other. This is the undercurrent of sexuality. It is the tension between part and whole. In TRIZ, which has a history in dialectical materialism, the task is to find and bring into ever more sharp contrast the basic physical contradiction. This provides the basis of insight and it also provides the ‘energy’ to produce new thinking. In the theory of dialogue, Patrick de Mare speaks of ‘hate’ (the dyad) leading to culture (the higher systems).

This stage is nearly always a critical one in working with a group. It is to notice and make use of conflict as a sign of the dyad. The dyad in its pure sense is not conflict, but we usually register it in these terms. Kierkegaard spoke of it as the either/or and said that it corresponded to the ethical. One form of the dyad is the contrast between fact and value. It is also the core of the question: What is real? For example, some people will say that only material existence is real, while others will say that only spiritual reality is really real! However, these general principles and insights are not enough. For every situation we take the hypothesis that there is one core dyad specific to it, even if we cannot agree what it is! After all the dyad will conform to itself and take contradictory forms.

It is not usual for us to deal with the dyad in its ‘naked’ sense. Either we revert back into the undifferentiating monad or we move forward into the reconciliation of the triad. Remaining in the dyad is hard to sustain without either of these moves or a collapse into mere conflict. Yet it is the main generator of energy. The state of togetherness of the two terms of the dyad is sometimes called simply ‘force’.

For every system, there is a corresponding mode of investigation and thought. Managing the transitions from one to another is a subtle art. This is for two main reasons. First of all, different people will be focussing — by temperament and habit — on different systems at the same time. Secondly, there are no set solutions for any system. The system is as it is seen by the people involved. As we said before, however, we can do a great deal to translate between different versions and bring all their diversity within a common form. This is not to produce a consensus but to evoke an experience of ‘sameness’ in all the different versions.

When it comes to the triadic stage, we look for what is capable of movement or change. We see that different things can combine to produce something new. We see the role of ‘catalysts’ facilitating a reaction. The affirmative forces are met with responses that ‘resist’ by seeking to conserve themselves and so we look for enabling forces that can produce a fusion between the two. This is roughly the same as ‘lateral thinking’. This is the basis of establishing the living network of the situation: everything is connected to everything else by means of something else. No two elements are connected in isolation. Here we see something of the nature of systems, in which there are not ‘connections’ apart from what is connected. The ‘third term’ is the connection of two others. Since our thinking tends to be dualistic — not the same as dyadic but a degenerate state of the dyad — we have the habit of thinking of two things connected and are not used to taking into account a third thing as integral to the mutual relevance of the two. Hence the value of such analogues as catalysis. The triadic stage of investigation also reveals everything as having different roles in different relationships.

Again, we take the hypothesis that there is one main triad governing the whole. This may be considered as having a ‘fractal’ nature, recurring throughout the given situation though on different scales and in different guises.

Each system affords its own way of investigation. It is a matter of coming to see the given form throughout a given complexity. One simple way of getting people to participate in this is to ask them to choose a given N number of elements as the ‘most important’ or the ‘most mutually meaningful’ from amongst the totality. This in itself is enough to bring people into the same frame of reference, without them having to know very much about what the system [N] ‘should’ be like. An important rule is to insist that the same terms used for one system are not carried over into another — though it cannot, in practice, be rigorously applied.

At the tetradic stage we look for four’s. Having elements we can arrange on a board is most useful. Such arrangements naturally take the form of ‘diamonds’ or ‘squares’ and it is then easy to think in terms of two pairs of oppositions. The tetrad concerns the maintenance of creativity and a balance of oppositions. In earlier times it was known as alchemy. We look for an intersection of ‘vertical’ and ‘horizontal’ interplays, a fusion of ‘ends’ and ‘means’. The ideal separates us from the actual (vertical), making a space for our own work. This work is the combination of theory and practice, or the masculine and the feminine (horizontal). Setting up a creative space requires four independent elements and we can explore what these might be in any given situation. David Kaplan points out that four roles are needed to produce a complete conversation. Every kind of action requires the co-operation of four modalities. Yet another analogue is provided by the heat engine that works in a cycle of four (and also reminds us that any working system must be open to energy flow). Engineering abounds with four’s : every technical system, according to TRIZ, must have an ‘engine’, ‘transmission’, ‘control unit’ and ‘working unit’. We can leap into psychology and think in terms of Jung’s four functions: sensation, intuition, thought and feeling.

The tetrad is ubiquitous and a large number of paradigms are available — as we have seen. For different audiences, different paradigms may be suitable. It is interesting that, even though the tetrad is so prevalent in so many areas of human experience and knowledge, we still have no means of ‘proving’ that four terms represent the universal structure of certain types of situation. The basic idea is that a tetrad is needed to maintain any whole in the midst of change. There has to be a pattern flexible enough to accommodate to what actually happens, and that allows for creativity. The system needs to be in contact with actuality. It is driven or directed by an agency and operated by an instrumentality.

At each successive stage, the situation under review appears more and more specific. This emerges strongly at the pentadic stage. Here we seek the ‘focus of significance’, that on which all else pivots, that which makes this situation what it is and through which it can become more. The pentad reveals the ‘heart’ of the situation. Also, at this stage, we can discriminate for the first time between the outer and inner conditions, or between the relatively immediate and the relative long-term, or between the smaller and the greater worlds involved. For example, an enterprise is a world of its own but could not exist without a larger whole in which it is embedded.

The situation has a unique identity by reason of some ‘essence’ that makes it so. In the case of an enterprise, this is the ‘task’ it commits itself to. Such a task should be more than survival, and is creative. Such a task has meaning in the greater whole of which the enterprise is a part. A simplistic guideline is that the core significance reveal both creative and mechanical aspects, and be relevant to both the relative chaos and the relative meaning of the greater whole. Thus an enterprise can serve the evolution of society by providing services to help manage its complexity.

The association of commitment with the pentad addresses its possible application to human enterprise and its management. But it serves to emphasise that the focus of significance is not something to be decided by an observer but only by a participant. The focus concerns the ‘will of the enterprise’ and not its functioning. It is the ‘more than survival’ attitude. The defining of a task is a creative step that has no meaning unless it is willed.

The further stages of investigation increasingly require the provision of paradigms as guidance. The hexadic stage concerns the coalescence of the smaller and the larger worlds indicated in the pentad. It is for example the creation of a new kind of business.

However, the simple principle that the series of systems can be extended without limit is of itself heuristic. In the most basic terms, systematics insists that there is always another step to be taken. Just knowing this is sufficient to inspire us to look around for insight into higher-term systems. To refer to TRIZ again, this is just as it is in innovation, where we can learn to draw on history and exercise creative imagination.

Application

Systematics concentrates on ‘seeing’ wholeness. In any concrete situation there is more involved. We suggest that there is a triad involved in which systematics is only one term.

	Systematics
Experience		Action

Experience is qualitative and includes the play of the unconscious. There is a kind of continuum in experience associated with the present moment. This eludes the strictures of systematics on both counts. The nature of the present moment involves uniqueness, while the continuum transcends structure.

In action we often have to do just one thing at any one time. A decision has to come down to a specific act.

We can of course regard systematics as mediating between experience and action. This it is useful to do. Nothing replaces our experience and all that is of value must come from it. At the same time, action needs to flow from our understanding and systematics is the form of understanding.

The character of systematics extends to similarities with other approaches. It is a form of analogous reasoning. It has similarities with traditional metaphorical understanding. For example, the landscape of clouds, mountains, streams, trees, winds, etc. can be taken as a landscape of the mind. In the Amerindian tradition, this is being recognised as ‘the language of the sensuous’, the language that is one with our perception of the world in which we walk. In this approach, the dominant mode is that of images. It is not for nothing that management consultants these days often have recourse to getting managers to draw or paint their situation rather than just talk about it.

The connection between number systems and images of, for example, rain falling from the clouds may seem obscure. Their ‘sameness’ is in recognising the ‘same’ in diverse situations. The rain falling from the clouds is taken as a symbol of divine mercy, or the way in which the substance from a higher world descends into our own. This understanding has a form that may not be spelled out in a number system but may reverberate with one. Think, for example, of the Chinese triad of Heaven-Man-Earth! But, the image gives us a great deal of information that renders our number system more alive and vivid in detail.

In the ancient system of the I Ching the abstract hexagrams are accompanied by images as well as commentary. Here is another working triad:

	Forms
Images		Commentary

It is fairly clear, then, that in practice number systems need the aid of metaphors and images to render them meaningful in our eyes. The three terms of the triad above reflect the three basic ways in which we come to understand the world:

FORMS:	abstract-gestural-kinaesthetic-mathematical	structure
IMAGES:	pictures-landscapes-feelings-metaphors	presence
COMMENTARY:	verbal-associative-conceptual-linear	process

Systematics is not to be separated from other modes. In his book Thought as a System David Bohm argues that we should not regard thought as a function separate from feeling, sensation, perception, communication, etc. It is all one whole. Nevertheless, thinking brings its own contribution to the whole and needs to be respected in its own right. It is also relevant to state that it is only when individuals are relatively independent and capable of self-initiative that they can come together in meaningful dialogue.

Summary

We have argued that there is a wealth of material supporting the proposition that all cultures of all times are involved in the thinking of number systems. Systematics begins with the simple notion that there are various ways of understanding our experience that can be coded according to the integers 1, 2, 3, etc. By this means we can access and bring together diverse material from many sources to illuminate what is of concern to us.

The systems [1], [2] etc. form a series that can be understood as a progression, or as steps of creativity. Each new system introduces something new. The basic idea that there is such a series may be enough to inspire us to search for greater and greater depth of meaning in what we are dealing with. Bennett postulated that the series has no end. Many others have proposed that this is not so and only a very few of the systems have any reality. There is no reason to accept such a limitation.

Each system is a ‘togetherness’ of independent terms. The nature of the system is determined by how many terms are mutually relevant. Hence a 4-fold system requires us to entertain four factors at once, while a 3-fold system requires only three, etc. In systematics it is supposed that the kind of ‘thinking’ needed for each system is specific to it and that thinking in 3’s is different from thinking in 4’s and so on. This is argued against in many quarters. However, it has at least an heuristic value in guiding us along the path of different orders of creativity.

Systems are rarely met in isolation from each other and the lower-number systems are implicitly nested in higher-number systems. This is to say that our understanding is always encompassed by a deeper understanding that draws us on. Thus some underlying concept of ‘higher intelligence’ as necessarily involved in our own stage of intelligence is implied in systematics. It also means that even lower-number systems ‘contain’ something of the higher-number ones.

It seems that different people favour different systems. Awareness of this can facilitate the handling of groups engaged on a common task and may also come to serve cross-cultural exchange.

There are different scales of systematics. There is for example a meta-level called N-grams in which the dominant ‘informing’ system is taken together with another associative system within a given number-base. In general, any system N is depicted within a range of NxN terms, allowing us to look into complex patterns of the internal structure. Thus, the triad [3] is seen in the 9-fold structure called the enneagram (as described by Gurdjieff). The dyad [2] appears in a 4-fold structure that represents the classic form of the tetrad. This is not strange since the dyad like any system ‘reflects on itself’ and has two versions of itself, and the triad has three versions of itself. It is not suitable here to go into this meta-level of systematics any further, except to say that it has application in any work of design.

By simply focussing on the 1-fold, 2-fold, 3-fold, etc. character of the series of systems it is possible to learn from examples in many fields. Systematics is inherently cross-disciplinary. Examples from engineering can be put side by side with examples from psychology. Every discipline seems to acquire its own systems, but they will be found to resonate across disciplines. The disciplines are arbitrary divisions while the systems are universal.

The elements or ‘terms’ of a system are not objects per se but are intentional. Hence, systems cannot be regarded as ‘models of the world’ if this world is taken in a mechanistic sense. Strong systems arise whenever truly independent people come together, constituting a ‘system of wills’. This concept has been applied to the generation of a series of N-loguesin which conversation is structured in N roles (to date the first four of these up to ‘tetralogue’ have been realised).

It is, of course, obvious that entertaining more than say four terms at once is taxing or rare. However, systematics says that this is only a contingent limitation and can be allowed for. N-logue shows us that people can participate in a greater whole, even without being able to be conscious of it — they are conscious in it. This corresponds with present thought on complex, emergent and self-organising systems where the ‘nodes’ are incapable of knowing all that is going on. People can experience at the level of sub-systems nested in higher-number systems.

Systematics challenges ‘observer-consciousness’ because the implied detached presence of the observer outside of the system breaks the system. At the same time, it is true that a witness of the given system as a whole then generates the novelty by which a higher-order system can actualise. This is the transition from the mute observer to the newly active participant. Systematics, then, is allied with dialogue as participative-process.

Though the most of systematics must remain unconscious and out of sight at any one time and set of circumstances, it is always informing the situation. We are constantly giving shape to our experience and tapping into the systems can accelerate this process and bring it to higher levels.

Systematics must become involved in images, actions and communication if it is to be vital and useful. It has been applied in education in the form of structural communication— long before the invention of N-logue — and takes its allegiance to the idea of the synergic epoch of co-operation that Bennett saw as an emergent feature of our world. Something of the nature of images has been taken up in the study of toponomics— the ‘rules of arrangement’. How we visualise the systems is most important.

The guiding principle is: only that which is independent and something in its own right can come together with other independencies in a co-operative venture into the unknown.

A Pictorial Evocation of Triadic Systems

contributed by James Patton and Jason Joslyn

“I can experience a hexad by looking at a shrub. I can see expansion in the growth of the shrub and concentration in the dying back of branches that grew in the wrong places. I see the effects of the interaction of sun, rain and wind on the shrub. I see its identity in the markings that show what family of plant it is. I see order in the symmetry, shape and structure of the plant, and I see freedom in the way in which this plant is different from any other plant on earth.”

– James Patton

Bibliography

A very few select titles by authors associated with John Bennett.

J. G. Bennett

• The Dramatic Universe Vols. I-4, especially Vol. III
• Elementary Systematics (edited by David Seamon)
• Deeper Man
• A Spiritual Psychology

A. G. E. Blake:

• The Monad
• The Dyad
• The Triad
• The Tetrad
• Systematics — a method of understanding complex wholes
• Systematics — a method of the intelligible & Toponomics
• Structures of Meaning
• The Intelligent Enneagram

H. Bortoft:

• The Wholeness of Nature — Goethe’s way of science

G. Gurdjieff:

• Beelzebub’s Tales to His Grandson

S. Kuchinsky:

• In Search of Miraculous Management

P. D. Ouspensky:

• In Search of the Miraculous
• Tertium Organum

S. Weightman:

• Religion as a Universe: the analogy with language, The Louis Jordan Occasional Papers in Comparative Religion No. 1

Major pioneers:

Pythagoras, Plato, Aristotle, Lull, Boehme, Leibnitz, Hegel

Modern authors:

Bohm, Peirce, Whitehead, Bertalanffy, Beer, Spencer-Brown, Jung, von Franz, Pensinger, Gebser, Wilber, Guenon, Smuts, Young, Bach, Fuller, de Mare, Pauli, Senge, Zwick, etc.

Best popular format book:

M. S. Schneider:

• A Beginner’s Guide to Constructing the Universe

Interesting Jungian view:

L. M. von Franz:

• Number and Time

Greatest mythical work:

G. I. Gurdjieff:

• Beelzebub’s Tales to His Grandson

Most extraordinary literary work:

William Pensinger and Nah Trang:

• The Moon of Hoa Binh

TRIZ method:

Y. Salamatov, edited by Valeri Souchkov, translated from the Russian by Maria Strogaia and Sergei Yakoviev

• TRIZ: The Right Solution at the Right Time. A guide to innovative problem solving.